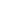什么是星形连接 (Y)?
星形连接(Y)系统也称为三相四线制(3-Phase 4 Wire),是交流配电的首选系统,而传输时通常使用三角形连接。
在星形(也用Y表示)互连系统中,三个线圈的始端或终点(相似端)连接在一起形成中性点。
星形连接是通过将三个线圈的相似端连接在一起获得的,“开始”或“结束”。另一端与线路连接。公共点称为中性点或星点,用N表示。(如图1所示)
星形连接也称为三相四线(3-Phase, 4-Wires)系统。
如果平衡对称负载并联连接在三相电压系统上,那么三个电流将流过中性线,它们的数量相同,但它们相差 120°(异相),因此这些电流的矢量和三电流 = 0. 即
I R + I Y + I B = 0 ……………。维多利亚时代
任意两个端子之间的电压或线与中性线(星点)之间的电压称为相电压 或星形电压,用V Ph表示。两条线之间的电压称为线间电压或线电压,用V L表示。
星形连接 (Y) 中的电压、电流和功率值
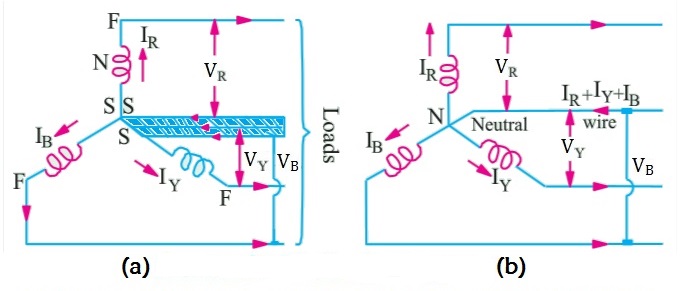
现在我们将找到三相星形交流系统中线电流、线电压、相电流、相电压和功率的值。
星形连接中的线电压和相电压
我们知道线 1 和线 2 之间的线电压(从图 3a)是
V RY = V R – V Y .... (矢量差)
因此,要找到 V RY的向量,在反方向增加 V Y的向量,如下图 2 中的虚线所示。同样,在向量 V R和向量 V Y 的两端,做垂直的虚线看起来像一个平行四边形,如图(2)所示。将平行四边形分成两部分的对角线,显示 V RY的值。V Y和 V之间的角度 R矢量是 60°。
因此,如果
V R = V Y = V B = V PH
然后
V RY = 2 x V PH x Cos (60°/2)
= 2 x V PH x Cos 30°
= 2 x V PH x (√3/2) …… 因为 Cos 30° = √3/2
V RY = √3 V PH
相似地,
V YB = V Y – V B
V YB = √3 V PH
和
V BR = V B – V R
V BR =√3V PH
因此,证明V RY = V YB = V BR是星形连接的线电压(V L),因此,星形连接;
V L = √3 V PH或 V L = √3 E PH
星形连接中的线电压和相电压
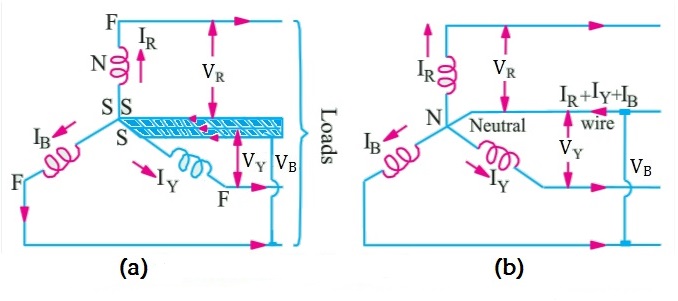
从图2中可以看出;
线电压彼此相距 120°
线电压与相应的相电压相差 30°
线电流与相应线电压的夹角Ф为(30°+Ф),即每条线电流都滞后(30°+Ф)相应的线电压。
星形连接中的线电流和相电流
从图(3a)可以看出,每条线都与单独的相绕组串联,因此,线电流值与线所连接的相绕组中的电流值相同。IE;
线路 1 中的电流 = I R
线路 2 中的电流 = I Y
线路 3 中的电流 = I B
由于三条线路中流动的电流相同,每条线路中的单个电流等于相应的相电流,因此;
I R = I Y = I B = I PH .... 相电流
线电流 = 相电流
I L = I PH
简单来说,线电流和相电流的值在星形连接中是相同的。
星形连接 (Y):线电流和电压值以及相电流和电压值
星形连接电源
在三相交流电源电路中,总有功或有功功率是三相功率之和。或者所有三相功率的总和是总有功功率或有功功率。
因此,三相交流系统中的总有功或有功功率;
总真功率或有功功率 = 3 相功率
或者
P = 3 x V PH x I PH x CosФ ..... Eq ... (1)
我们知道星形连接的相电流和相电压值;
I L = I PH
V PH = V L /√3 .....(来自V L = √3 V PH)
将这些值放在功率方程中...... (1)
P = 3 x (V L /√3) x I L x CosФ …….. (V PH = V L /√3)
P = √3 x√3 x (V L /√3) x I L x CosФ ..... {3 = √3x√3}
P = √3 x V L x I L x CosФ
因此证明;
星形连接电源,
P = 3 x V PH x I PH x CosФ 或
P = √3 x V L x I L x CosФ
同样的解释在 3-Phase Circuit MCQs with anexplanatory Answer (MCQs No.1) 中也有同样的解释
相似地,
总无功功率 = Q = √3 x V L x I L x SinФ
其中Cos Φ = 功率因数= 相电压和相电流之间的相角,而不是线电流和线电压之间的相角。
很高兴知道:感应线圈的无功功率被视为正极 (+),电容器的无功功率被视为负极 (-)。
此外,三相的总视在功率;
总视在功率 = S = √3 x V L x I L或,
S = √ (P 2 + Q 2 )。